3 Super Tips for Teaching Place Value
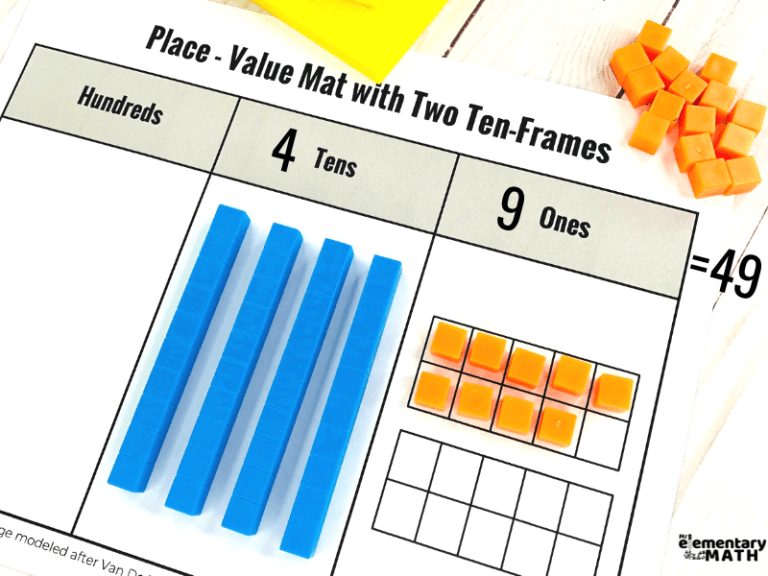
Here’s the understatement of the year: teaching place value is kind of a big deal! From kindergarten through 5th grade, “Numbers and Operations in Base
Take the stress out of implementing math centers in your classroom...
