Today, I want to discuss the importance of using number lines with students to get them to conceptually understand fractions. Number Lines are such great tools because they provide clear visual images that assist students in developing the concept of number magnitude. According to Moss and Case (1999), a number line is a mathematical model that provides a rich environment for understanding and reasoning about rational numbers.
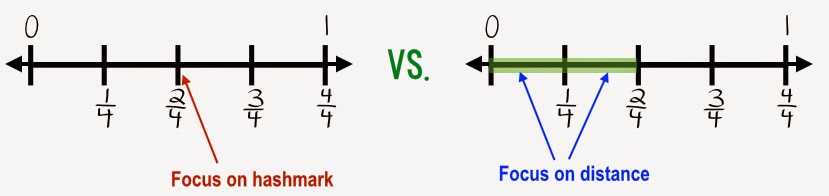
Much like a ruler, a number line is a linear scale that is divided into equal distances. Oftentimes, as educators we teach students to only read the hashmarks on a number line, but one of the most important things to understand is the distance from 0 to a designated point.
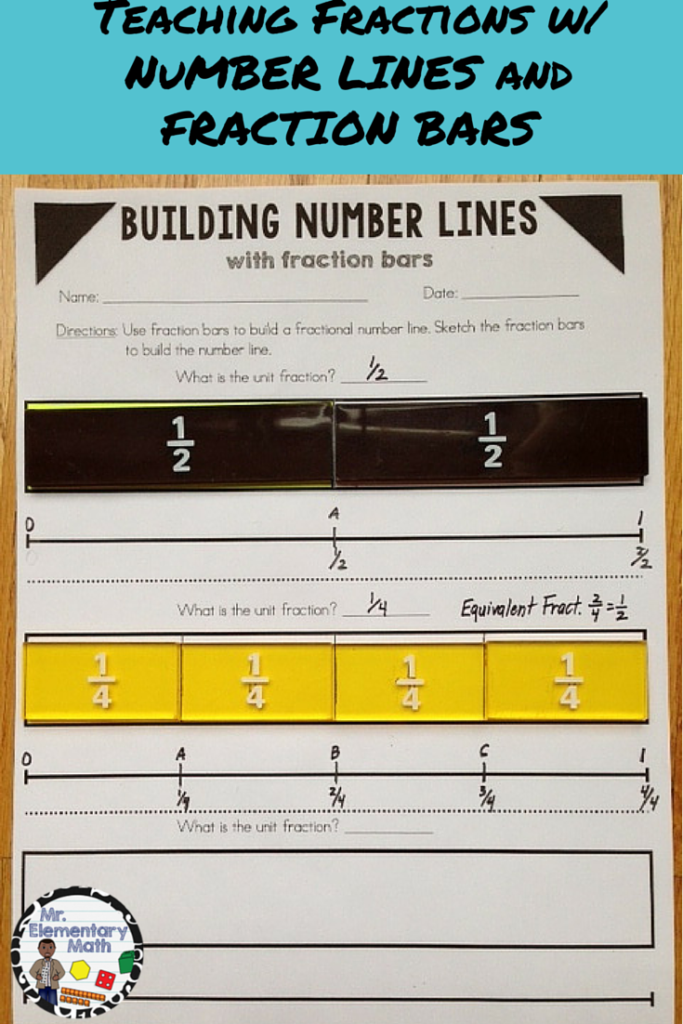
To help students better understand this concept I have students build number lines with fraction bars. We start by using fraction bars to determine how many parts will make up the whole rectangle. We then partition the rectangle into equal parts and apply the same concept to the number line. Check out the example below.
Guiding questions that are helpful when doing this activity include:
* What is the unit fraction that you are working with?
* How many unit fractions make up the whole?
* Explain how the fraction bar and number line are similar? Different?
* What is the distance from 0 to point A? Point A to B? Point B to C? etc.
* What is the distance from 0 to point A? 0 to point B? 0 to point C? etc.
As an extension, students can find fractions that are equivalent and discuss what they notice. For example, in the image above the distance from 0 to point A (top number line) is 1/2 and the distance from 0 to point B (bottom number line) is 2/4. The distance from 0 to both points are the same, therefore 1/2 and 2/4 are equivalent.
This activity helps students better understand:
* how to partition rectangles and number lines
* fraction sizes
* unit fractions that make up a whole
* how to decompose and compose fractions
* fraction equivalency
Check out the completed version of the activity below.
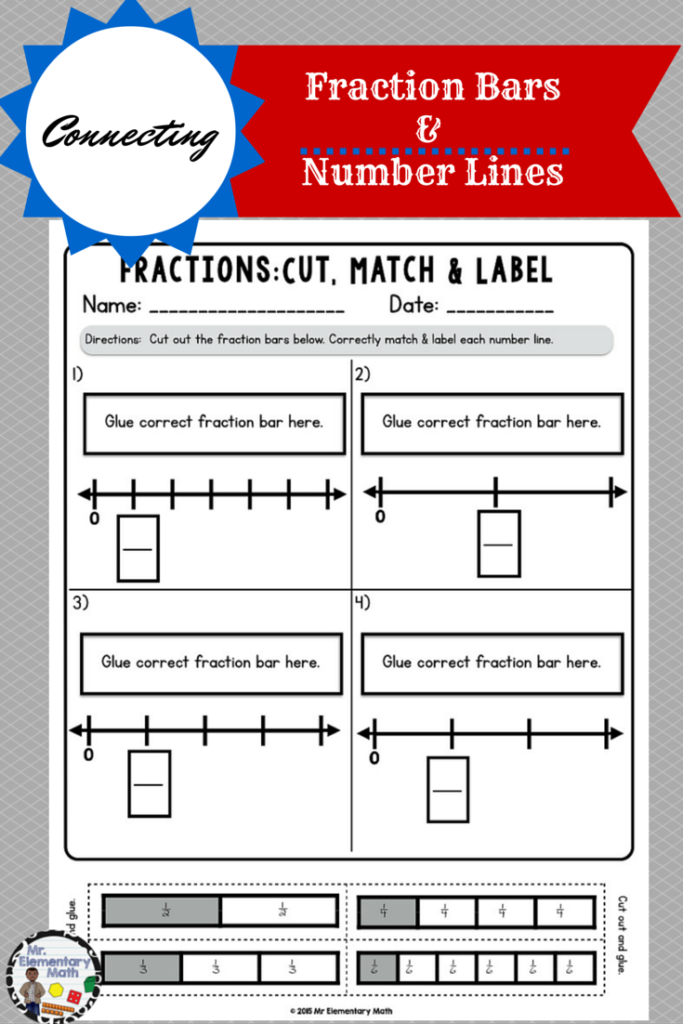
I also use the activity sheet below to further reinforce this understanding.
Hopefully this was a helpful post to bridge the understanding between fractions and building number lines.If you are looking for more resources for teaching fractions using numbers, click on the photo below to check on Fraction Games and Activities Using Models and Number Lines.