Fly on a Math Teachers Wall: Place Value

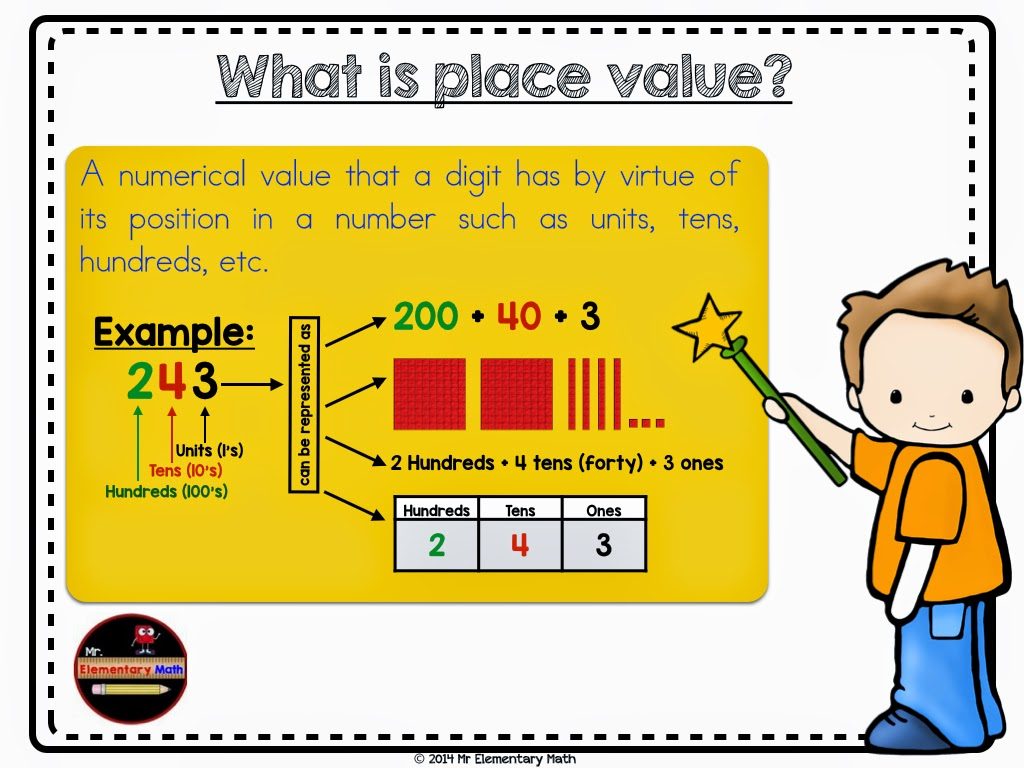
Place Value is such an important topic but many of our students have a difficult time understanding and applying it.

Today my focus will be on using place value charts to compare numbers.  Let’s start with a definition of place value.

Mastery of place value leads to greater understanding of the following topics:  decimals, rounding, addition, subtraction, ordering numbers and so much more.

Place Value in Primary Grades

As many of us know, comparing numbers is a difficult concept for our students. Oftentimes in the primary grades, students explore number comparisons using an “alligator mouth”. Basically the “alligator mouth” acts as the greater or less than sign.

I know this will be a controversial statement but, “when comparing numbers, the sole focus shouldn’t be on an alligator eating the larger number.” You maybe asking why?

Comparing numbers is truly about understanding why one number is larger than the other through exploration and examination of each digit in a number and understanding the value the digit holds.

• 1 ten (the smallest 2 digit number) is greater than any amount of ones represented by a one-digit number; thus we compare 2 digit numbers by looking at the tens place first.
• 1 hundred (the smallest 3 digit number) is greater than any amount of tens and ones represented by a two-digit number; thus we compare 3 digit numbers by looking at the hundreds place first.
• 1 thousand (the smallest 4 digit number) is greater than any amount of hundreds, tens and ones represented by a three-digit number; thus we compare 4 digit numbers by looking at the thousands place first.

To support this concept, I typically use place value charts.

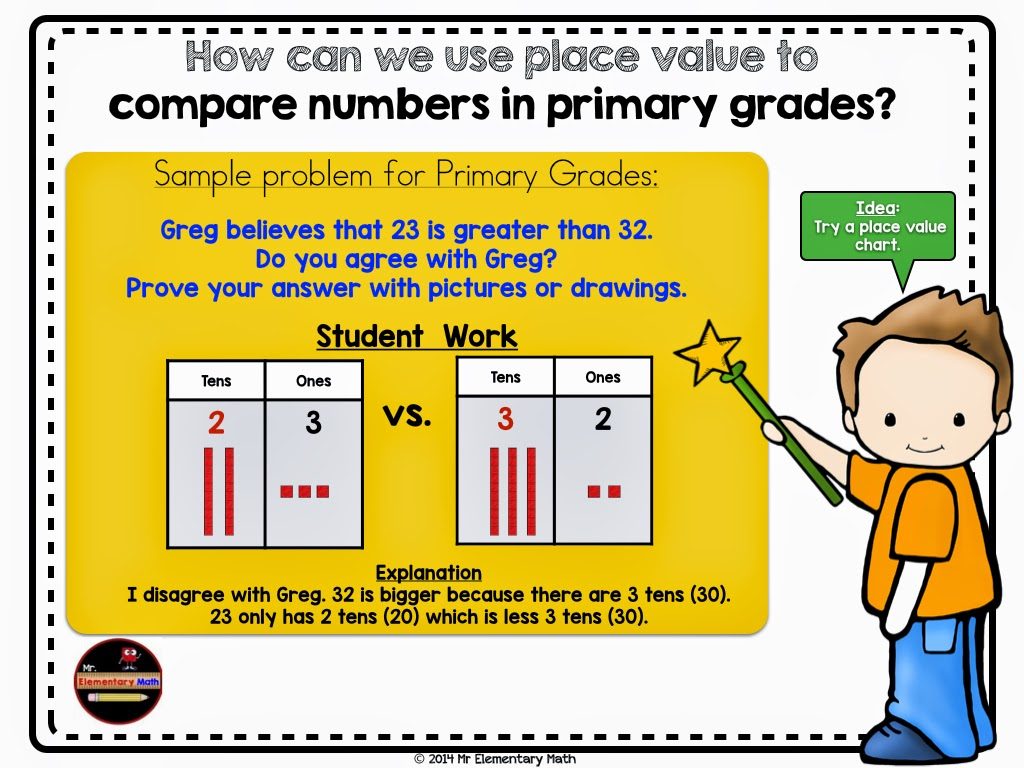
Below you will find an example where place value charts are used to compare numbers in the primary grades.

Using base ten blocks within a place value chart helps students understand that 32 is larger than 23 because 3 tens is larger than 2 tens.  

If you do not have base ten blocks, connecting cubes are also another good tool.  It is critical that students provide an explanation that supports their findings.

Two important questions that can guide this work include:

• How are _____   and _____ alike?  Prove it by showing me.
• How are _____   and _____ different? Prove it by showing me.  

I have been talking a lot about comparing numbers for primary grades, I am sure that upper grades teachers are wondering, “How does this help me?”  Check out the comparing numbers problem below.

Place Value in Upper Grades

Notice how the place value chart was used to compare the numbers.  Instead of using base ten models the numbers are written in expanded form.  When comparing multi-digit numbers, using expanded form to examine how numbers in each place are alike and different is a great strategy.   Looking at numbers in this way really gets to the root of why one number is greater or less than the other.

 

Explanations and justifications are a critical part of this work.  In the example above, you will notice that 6,818, 6,801 and 6,881 have the same amount of thousands and hundreds. The three numbers are different because they have different amounts of tens and ones.  

 

Using the place value chart, as a tool, allows the student to see the patterns mentioned above and determine that the number with 0 tens must be the smallest (6,801).  The number with 1 ten (6,818) is larger than the number with 0 tens (6,801) because 1 ten is more than 0 tens.  Lastly, 6,881 is the largest number because 8 tens is greater than 1 ten and 0 tens; therefore Mike is not correct.

 

To support your students with comparing numbers, download the place value comparison chart below. Click to grab it now  Free Place Value Comparison Chart. 

 

 

If you have not used place value charts in this way before, I encourage you to try them out!

I hope you enjoyed this post.

33