Properties of Operations are those three pesky words that reoccur throughout the common core standards. Some of you may be wondering exactly what they mean. Properties of Operations are the foundation of arithmetic; we use them when performing computations and recalling basic facts.
In this post, I will focus on the following 3 properties that are used with addition and multiplication:
- Commutative Property
- Associative Property
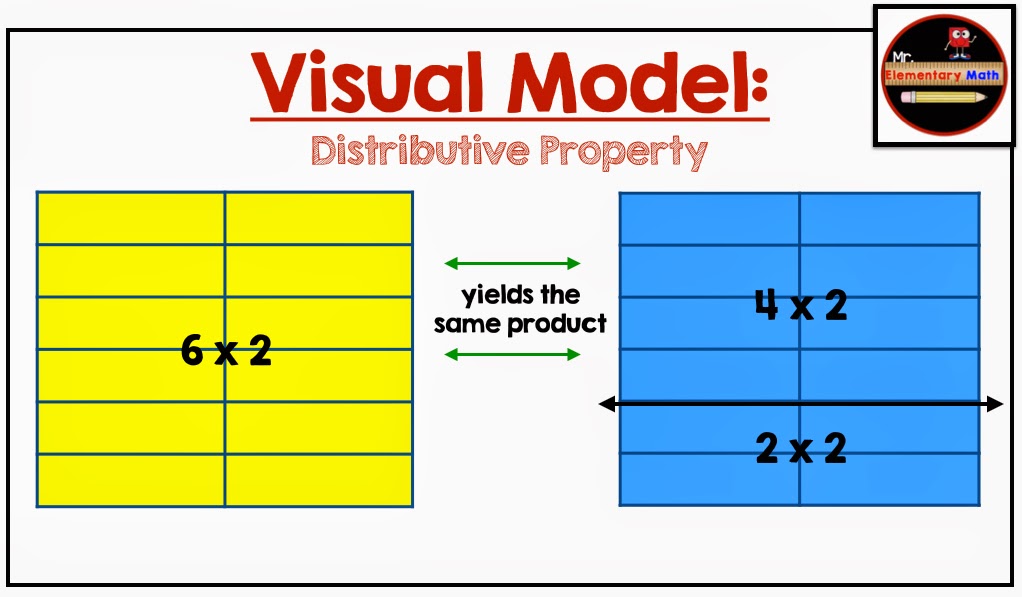
- Distributive Property
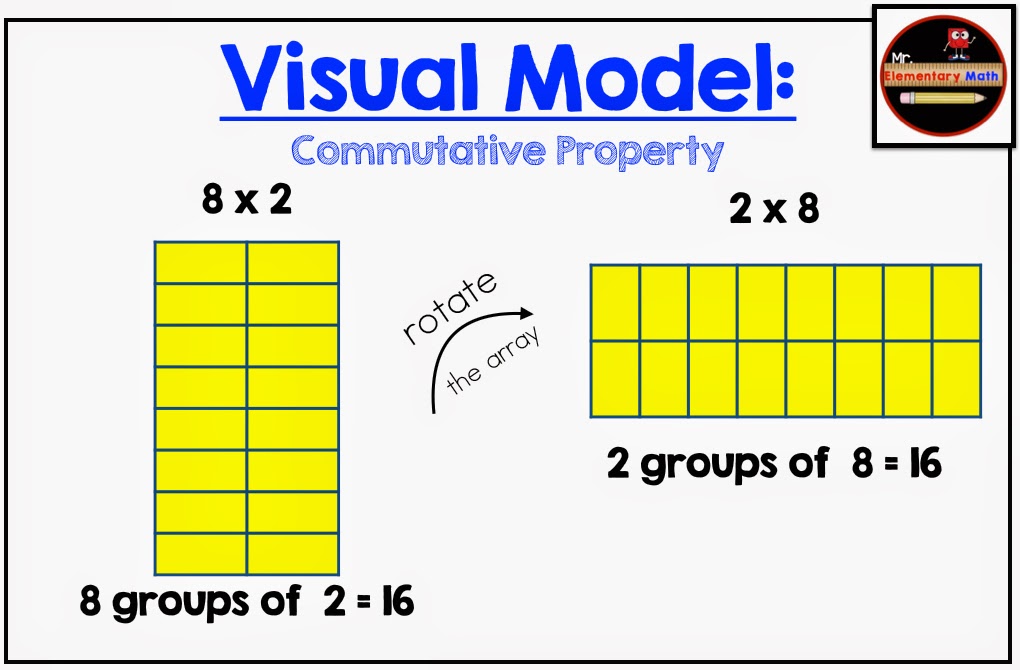
An idea to help with the commutative property may be:
- Providing students with tiles or counters and asking them to model 8 x 2 & 2 x 8; 3 x 4 & 4 x 3, 5 x 3 & 3 x5. Then ask the students to compare the product of each factor pair (ie. 8 x 2 and 2 x 8). Students should be able to explain that the products are identical. To sum it up, students should model, model, model multiplication equations in any order to see if the products are always identical.
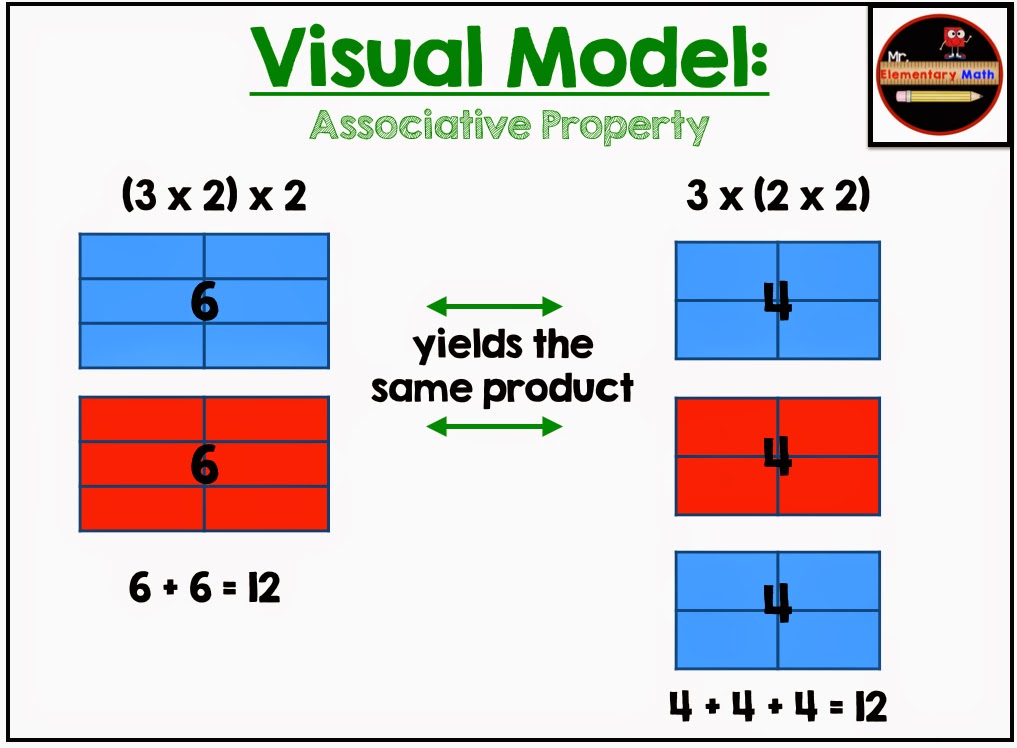
Next, the associative property states that changing the grouping of the factors does not change the product. This property works closely with the commutative property because we often change the order of groupings of factors when multiplying numbers to make it easier to solve problems.
Using 3 x 2 x 2 as the basis of our groupings, below you will see a visual model of how the associative property works.
- Providing the students with counters or tiles and asking them to model (3 x 2) x 2 and then 3 x (2 x 2); like the example above. From this point allow the students to determine patterns they notice. Consider asking the students: What is the product of both expressions? Why do they think the product is the same for both? Try this investigation with different expressions including: (5 x 2) x 2 and 5 x (2 x 2), (3 x 4) x 2 and 3 x (4 x 2). Students should begin to generalize that changing the groupings does not change the product.
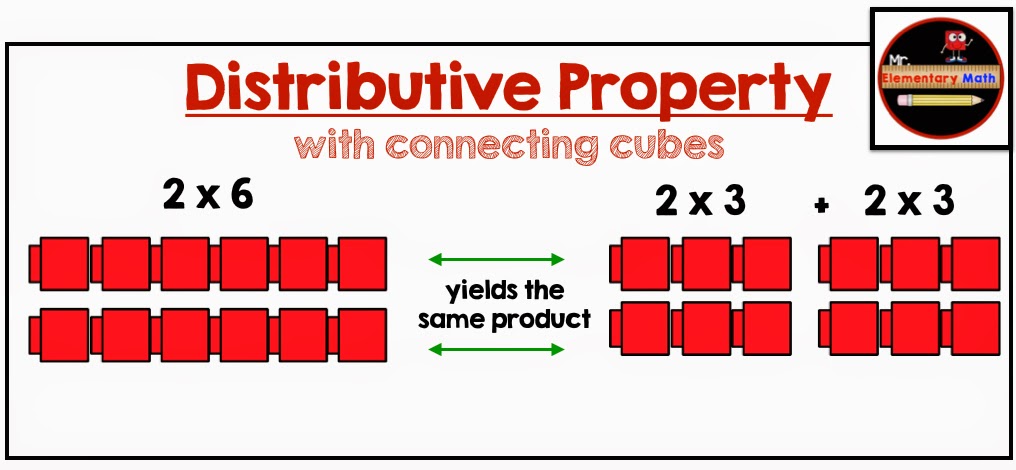
- Asking students to model 2 groups of 6 (2 x 6) using connecting cubes and find two hidden facts inside of 2 x 6 like 2 x 3 and 2 x 3. Allow the students time to discover as many hidden facts inside of the 2 x 6 that they can. Try this out with different multiplication facts through 10 x 10. Do not forget to ask students what they notice as they are doing this investigation.