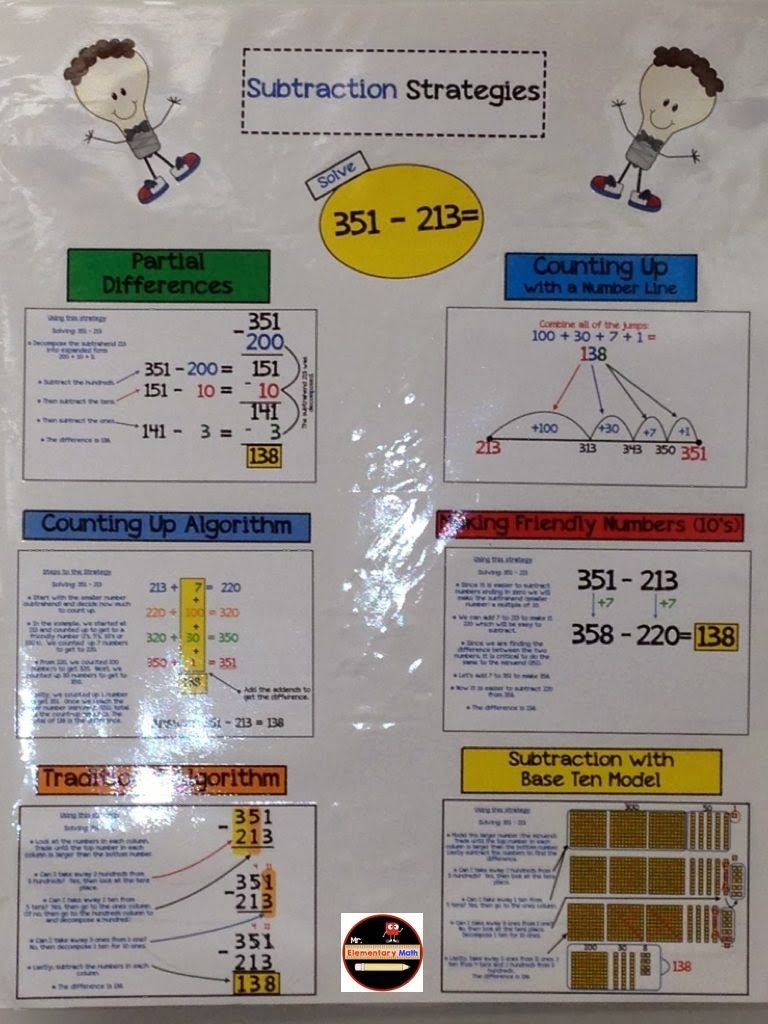
Subtraction has always been a topic of interest to me. As a teacher I remember teaching the traditional algorithm like the one in the image below.
I talked to my children about borrowing a ten from the 5 to add to the 1. It was an interesting thing because though I used the traditional algorithm I really didn’t have a deepened conceptual understanding of it. I simply went through the process with my students. It wasn’t until years later that I had an Ahh Haa.. moment!
The regrouped number 351( 3 hundreds + 4 tens + 11 ones) or (300 + 40 + 11) is equal to the original number of 351. We simply renamed the number to make it easier to take away 213!
As I reflect on my own understanding, I often think why did I continue to use the traditional algorithm. When I assessed my class, the majority of my students got the answer to the subtraction problem correct using the traditional algorithm, but during classroom discussions they did not have a deepened conceptual understanding. At the time, I really didn’t have any other strategies but to reteach the same concept using base ten blocks.
Five years ago, while at a grocery store I bought donuts that cost $5.69. I gave the cashier a $10 bill. I had been reading about mental math strategies and I attempted to figure out the amount of change that I should receive before the cashier gave it back to me. So I started to count up from $5.69 until I reached $10. The steps that I did mentally to get to the nearest ten or dollar included:
- I was 1 cent away from $5.70
- From there I needed to get to $6.00 which was 30 cent away
- Now I could count by $1 bills… starting at $6.00. I counted up until I reached $10.
- There were $4 to reach $10.
- Lastly I combined all of the amounts, 1 cent + 30 cent + $4 dollars to get…… $4.31
If counting up in my head is an easy strategy to subtract numbers, why not teach this strategy to our students? Counting up is an amazing strategy that reinforces the relationship between numbers. Believe me, I know the traditional algorithm is a familiar technique but we should consider other ways to make subtraction an accessible operation for our children.
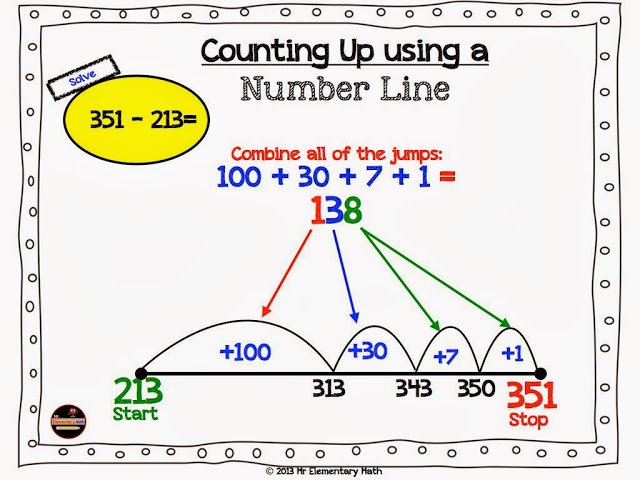
Number lines are awesome tools to introduce this. Let’s use the number line to help with the example in the image above.
- We started at 213, then skipped 100 numbers to get to 313.
- Next, we skipped 30 more numbers to land on 343.
- Then, we skipped 7 numbers to land on 350.
- Last, we skipped 1 number to reach 351.
- Combine all the jumps to get the distance between 213 and 351.
I would like to challenge you to try this strategy when teaching subtraction to your students. If you decide to use it, please describe your experience in the comments section.
For more subtraction strategies check out the TpT product below by clicking on the link:
70